

Make the most out of your models
modelbased is a package helping with model-based estimations, to easily compute marginal means, contrast analysis and model predictions.
The two probably most popular R packages for extracting these quantities of interest are emmeans (Lenth, 2024) and marginaleffects (Arel-Bundock et al., 2024). These packages pack an enormously rich set of features and cover (almost) all imaginable needs for post-hoc analysis of statistical models. But their power and flexibility can be intimidating for users not familiar with the underlying statistical concepts.
modelbased, built on top of these two packages, aims to unleash this untapped potential by providing a unified interface to extract marginal means, marginal effects, contrasts, comparisons, and model predictions from a wide range of statistical models. In line with the easystats’ raison d’être, modelbased focuses on simplicity, flexibility, and user-friendliness to help researchers harness the full power of their models.
How to start?
The package’s approach simplifies estimation by focusing on three key questions:
Predictor of Interest: Which variable’s effect do you want to
analyze? This is specified with the by,
contrast, or trend arguments.
Evaluation Points: At which specific values should the predictor
be evaluated? This is also defined in the by argument. For
a more refined control over the evaluation points, see the data
grids vignette.
Target Population: What population should the inferences
generalize to? The estimate argument controls this by
defining whether predictions are for a typical individual, an average of
the sample, or an average of a broader population.
The modelbased package is available on CRAN, while its latest development version is available on R-universe (from rOpenSci).
| Type | Source | Command |
|---|---|---|
| Release | CRAN | install.packages("modelbased") |
| Development | R-universe | install.packages("modelbased", repos = "https://easystats.r-universe.dev") |
Once you have downloaded the package, you can then load it using:
library("modelbased")Tip:
Instead of
library(modelbased), uselibrary(easystats). This will make all features of the easystats-ecosystem available.To stay updated, use
easystats::install_latest().
Access the package documentation, and check-out these vignettes:
The core idea behind the modelbased package is that statistical models often contain a lot more insights than what you get from simply looking at the model parameters. In many cases, like models with multiple interactions, non-linear effects, non-standard families, complex random effect structures, the parameters can be hard to interpret. This is where the modelbased package comes in.
To give a very simply example, imagine that you are interested in the
effect of 3 conditions A, B and C on a
variable Y. A simple linear model Y ~ Condition
will give you 3 parameters: the intercept (the average value of
Y in condition A), and the relative effect of
condition B and C. But what you would like to also get
is the average value of Y in the other conditions too. Many
people will compute the average “by hand” (i.e., the empirical
average) by directly averaging their observed data in these groups.
But did you know that the estimated average (which can be much
more relevant, e.g., if you adjust for other variables in the model) is
contained in your model, and that you can get them easily by running
estimate_means()?
The modelbased package is built around 4 main functions:
estimate_means():
Estimates the average values at each factor levelsestimate_contrasts():
Estimates and tests contrasts between different factor levelsestimate_slopes():
Estimates the slopes of numeric predictors at different factor levels or
alongside a numeric predictorestimate_prediction():
Make predictions using the modelThese functions are based on important statistical concepts, like data grids, predictions and marginal effects, and leverages other packages like emmeans and marginaleffects. We recommend reading about all of that to get a deeper understanding of the hidden power of your models.
Check-out the function documentation and this vignette for a detailed walkthrough on marginal means.
library(modelbased)
library(ggplot2)
# 1. The model
model <- lm(Sepal.Width ~ Species, data = iris)
# 2. Obtain estimated means
means <- estimate_means(model, by = "Species")
means
## Estimated Marginal Means
##
## Species | Mean | SE | 95% CI | t(147)
## ------------------------------------------------
## setosa | 3.43 | 0.05 | [3.33, 3.52] | 71.36
## versicolor | 2.77 | 0.05 | [2.68, 2.86] | 57.66
## virginica | 2.97 | 0.05 | [2.88, 3.07] | 61.91
##
## Variable predicted: Sepal.Width
## Predictors modulated: Species
# 3. Custom plot
ggplot(iris, aes(x = Species, y = Sepal.Width)) +
# Add base data
geom_violin(aes(fill = Species), color = "white") +
geom_jitter(width = 0.1, height = 0, alpha = 0.5, size = 3) +
# Add pointrange and line for means
geom_line(data = means, aes(y = Mean, group = 1), linewidth = 1) +
geom_pointrange(
data = means,
aes(y = Mean, ymin = CI_low, ymax = CI_high),
size = 1,
color = "white"
) +
# Improve colors
scale_fill_manual(values = c("pink", "lightblue", "lightgreen")) +
theme_minimal()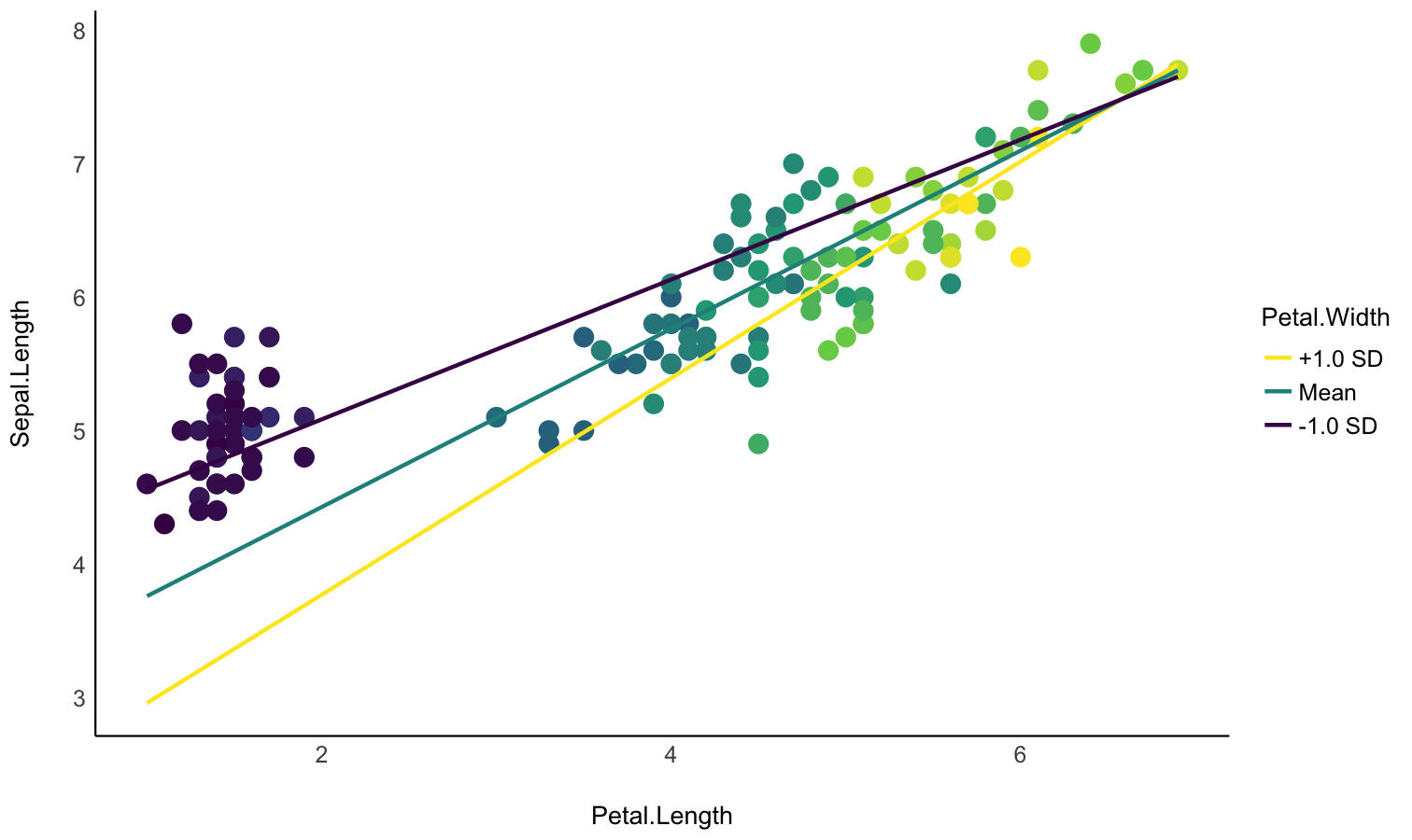
You can also get a “quick” plot using the plot()
function:
plot(means)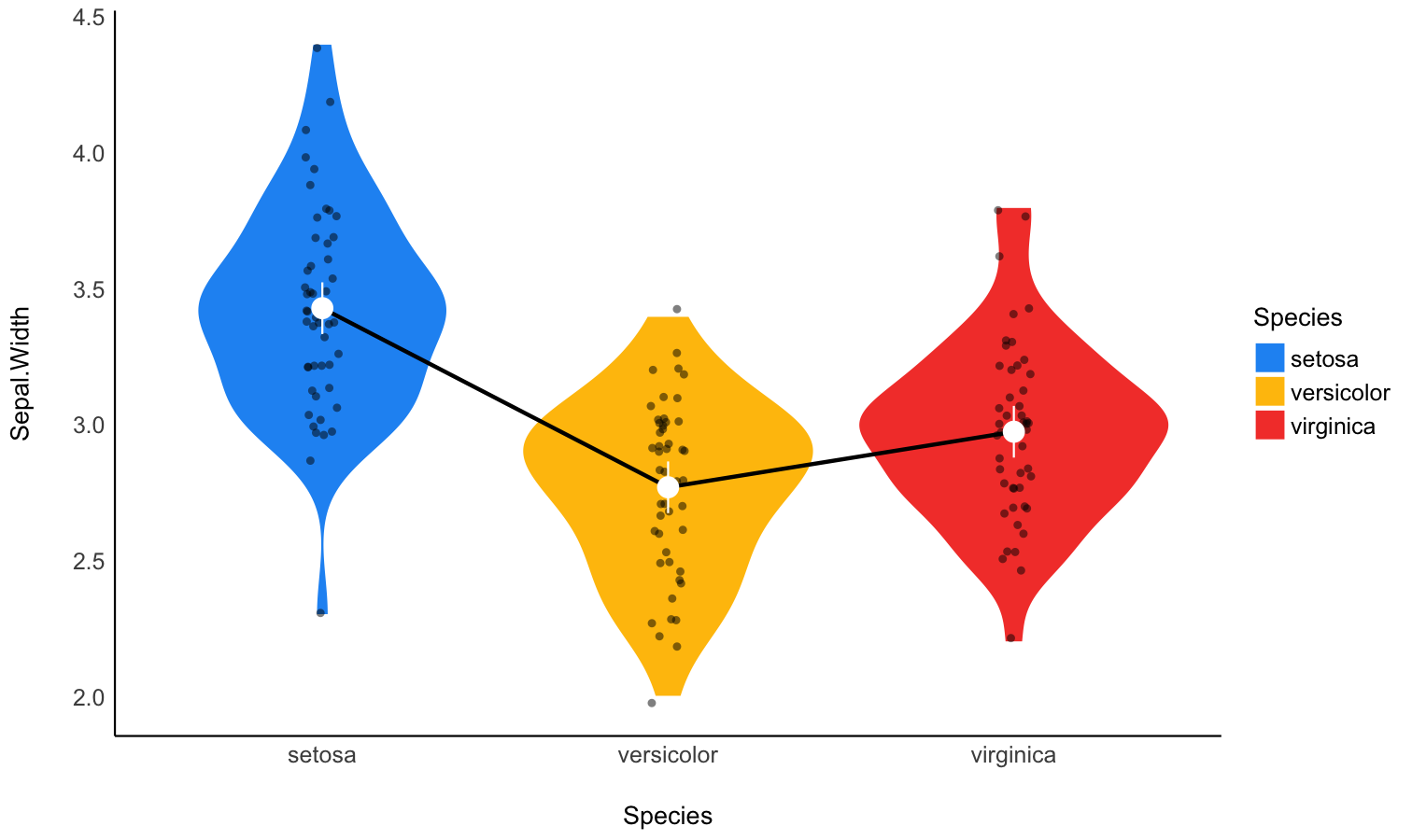
Check-out this vignette for a detailed walkthrough on contrast analysis.
# 1. The model
model <- lm(Sepal.Width ~ Species, data = iris)
# 2. Estimate marginal contrasts
contrasts <- estimate_contrasts(model, contrast = "Species")
contrasts
## Marginal Contrasts Analysis
##
## Level1 | Level2 | Difference | SE | 95% CI | t(147) | p
## ------------------------------------------------------------------------------
## versicolor | setosa | -0.66 | 0.07 | [-0.79, -0.52] | -9.69 | < .001
## virginica | setosa | -0.45 | 0.07 | [-0.59, -0.32] | -6.68 | < .001
## virginica | versicolor | 0.20 | 0.07 | [ 0.07, 0.34] | 3.00 | 0.003
##
## Variable predicted: Sepal.Width
## Predictors contrasted: Species
## p-values are uncorrected.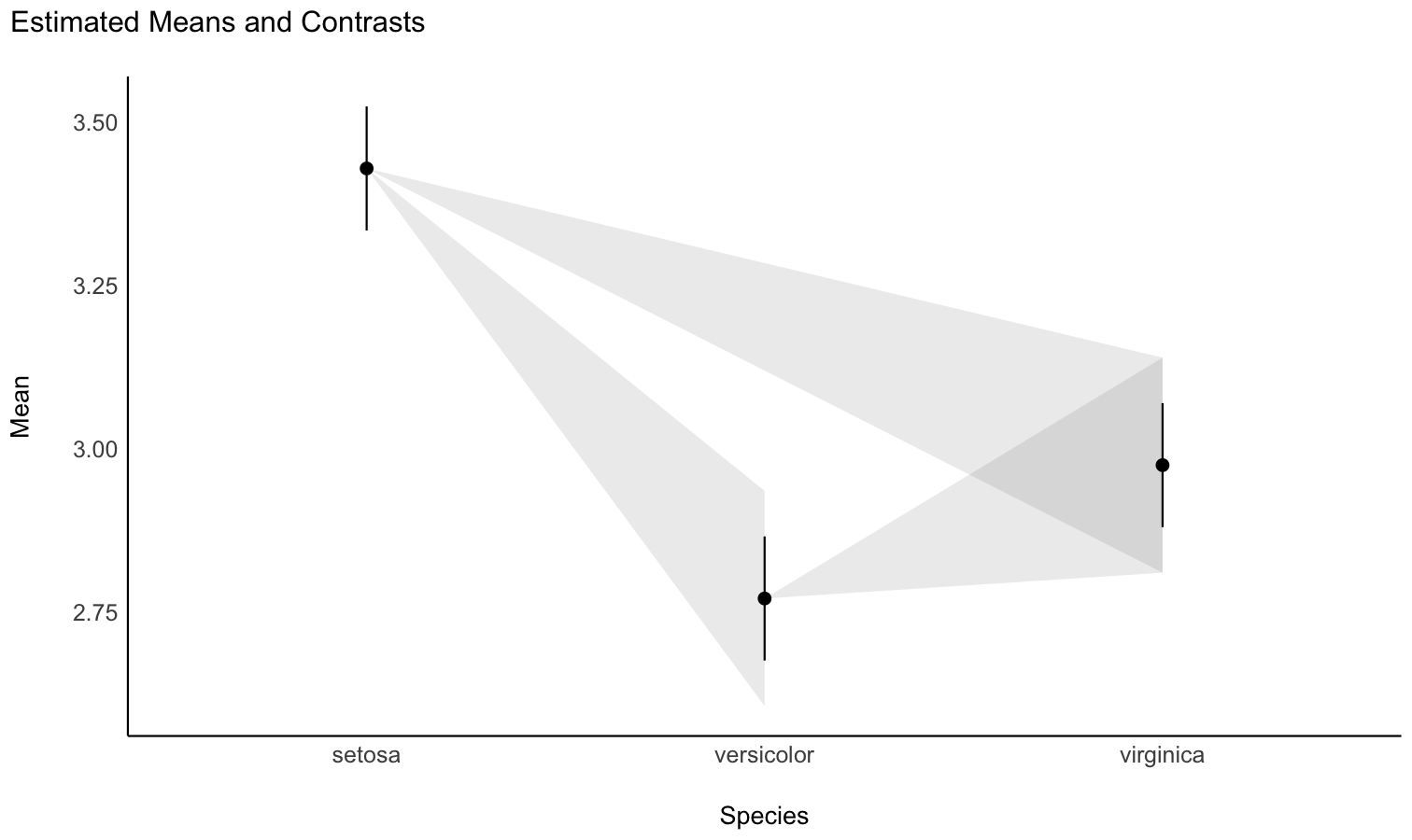
model <- lm(Sepal.Width ~ Species * Petal.Length, data = iris)
difference <- estimate_contrasts(
model,
contrast = "Species",
by = "Petal.Length",
length = 3
)
# no line break for table
print(difference, table_width = Inf)
## Marginal Contrasts Analysis
##
## Level1 | Level2 | Petal.Length | Difference | SE | 95% CI | t(144) | p
## ---------------------------------------------------------------------------------------------
## versicolor | setosa | 1.00 | -1.70 | 0.34 | [-2.37, -1.02] | -4.97 | < .001
## virginica | setosa | 1.00 | -1.34 | 0.40 | [-2.13, -0.56] | -3.38 | < .001
## virginica | versicolor | 1.00 | 0.36 | 0.49 | [-0.61, 1.33] | 0.73 | 0.468
## versicolor | setosa | 3.95 | -1.74 | 0.65 | [-3.03, -0.45] | -2.67 | 0.008
## virginica | setosa | 3.95 | -1.79 | 0.66 | [-3.11, -0.48] | -2.70 | 0.008
## virginica | versicolor | 3.95 | -0.06 | 0.15 | [-0.35, 0.24] | -0.37 | 0.710
## versicolor | setosa | 6.90 | -1.78 | 1.44 | [-4.62, 1.06] | -1.24 | 0.218
## virginica | setosa | 6.90 | -2.25 | 1.42 | [-5.06, 0.56] | -1.58 | 0.116
## virginica | versicolor | 6.90 | -0.47 | 0.28 | [-1.03, 0.09] | -1.65 | 0.101
##
## Variable predicted: Sepal.Width
## Predictors contrasted: Species
## p-values are uncorrected.# Recompute contrasts with a higher precision (for a smoother plot)
contrasts <- estimate_contrasts(
model,
contrast = "Species",
by = "Petal.Length",
length = 20,
# we use a emmeans here because marginaleffects doesn't
# generate more than 25 rows for pairwise comparisons
backend = "emmeans"
)
# Add Contrast column by concatenating
contrasts$Contrast <- paste(contrasts$Level1, "-", contrasts$Level2)
# Plot
ggplot(contrasts, aes(x = Petal.Length, y = Difference, )) +
# Add line and CI band
geom_line(aes(color = Contrast)) +
geom_ribbon(aes(ymin = CI_low, ymax = CI_high, fill = Contrast), alpha = 0.2) +
# Add line at 0, indicating no difference
geom_hline(yintercept = 0, linetype = "dashed") +
# Colors
theme_modern()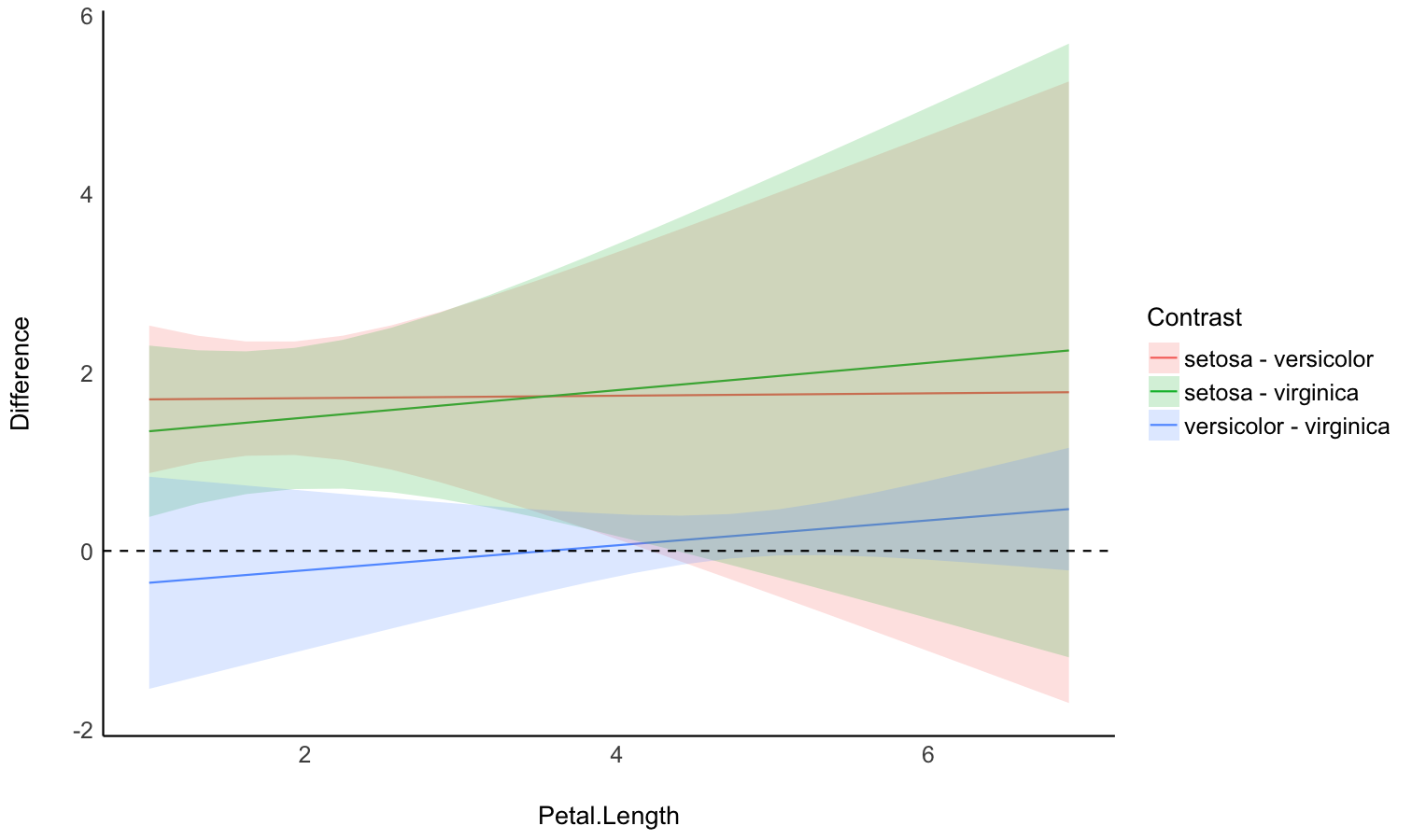
Check-out this vignette for a detailed walkthrough on visualisation matrices.
# 1. Fit model and get visualization matrix
model <- lm(Sepal.Length ~ Petal.Length * Petal.Width, data = iris)
# 2. Create a visualisation matrix with expected Z-score values of Petal.Width
vizdata <- insight::get_datagrid(model, by = c("Petal.Length", "Petal.Width = c(-1, 0, 1)"))
# 3. Revert from expected SD to actual values
vizdata <- unstandardize(vizdata, select = "Petal.Width")
# 4. Add predicted relationship from the model
vizdata <- modelbased::estimate_expectation(vizdata)
# 5. Express Petal.Width as z-score ("-1 SD", "+2 SD", etc.)
vizdata$Petal.Width <- effectsize::format_standardize(vizdata$Petal.Width, reference = iris$Petal.Width)
# 6. Plot
ggplot(iris, aes(x = Petal.Length, y = Sepal.Length)) +
# Add points from original dataset (only shapes 21-25 have a fill aesthetic)
geom_point(aes(fill = Petal.Width), size = 5, shape = 21) +
# Add relationship lines
geom_line(data = vizdata, aes(y = Predicted, color = Petal.Width), linewidth = 1) +
# Improve colors / themes
scale_color_viridis_d(direction = -1) +
scale_fill_viridis_c(guide = "none") +
theme_minimal()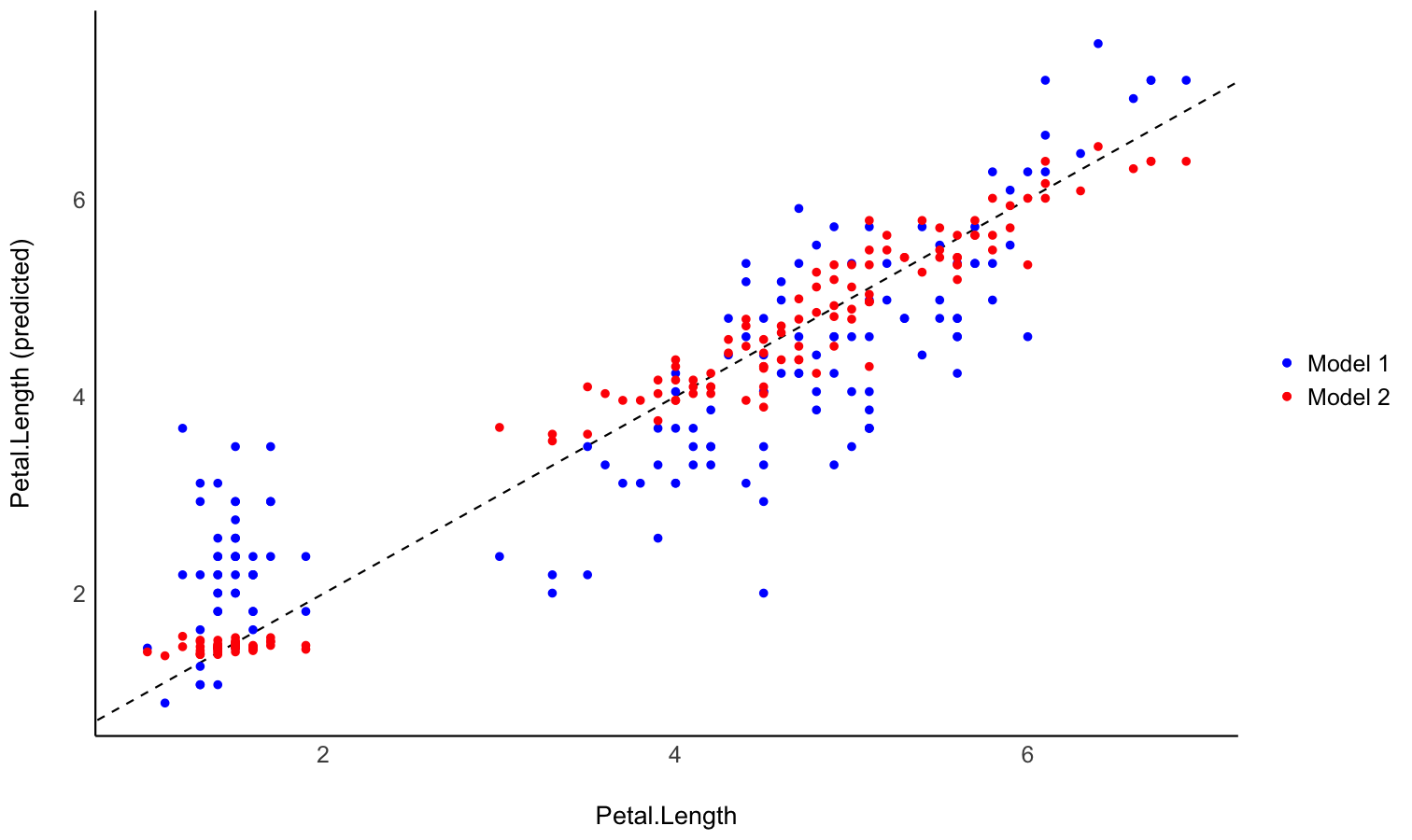
Check-out this vignette for a detailed walkthrough on predictions.
# Fit model 1 and predict the response variable
model1 <- lm(Petal.Length ~ Sepal.Length, data = iris)
pred1 <- estimate_expectation(model1)
pred1$Petal.Length <- iris$Petal.Length # Add true response
# Print first 5 lines of output
head(pred1, n = 5)
## Model-based Predictions
##
## Sepal.Length | Predicted | SE | 95% CI | Residuals | Petal.Length
## -------------------------------------------------------------------------
## 5.10 | 2.38 | 0.10 | [2.19, 2.57] | -0.98 | 1.40
## 4.90 | 2.00 | 0.11 | [1.79, 2.22] | -0.60 | 1.40
## 4.70 | 1.63 | 0.12 | [1.39, 1.87] | -0.33 | 1.30
## 4.60 | 1.45 | 0.13 | [1.19, 1.70] | 0.05 | 1.50
## 5.00 | 2.19 | 0.10 | [1.99, 2.39] | -0.79 | 1.40
##
## Variable predicted: Petal.Length
# Same for model 2
model2 <- lm(Petal.Length ~ Sepal.Length * Species, data = iris)
pred2 <- estimate_expectation(model2)
pred2$Petal.Length <- iris$Petal.Length
# Initialize plot for model 1
ggplot(data = pred1, aes(x = Petal.Length, y = Predicted)) +
# with identity line (diagonal) representing perfect predictions
geom_abline(linetype = "dashed") +
# Add the actual predicted points of the models
geom_point(aes(color = "Model 1")) +
geom_point(data = pred2, aes(color = "Model 2")) +
# Aesthetics changes
labs(y = "Petal.Length (predicted)", color = NULL) +
scale_color_manual(values = c("Model 1" = "blue", "Model 2" = "red")) +
theme_modern()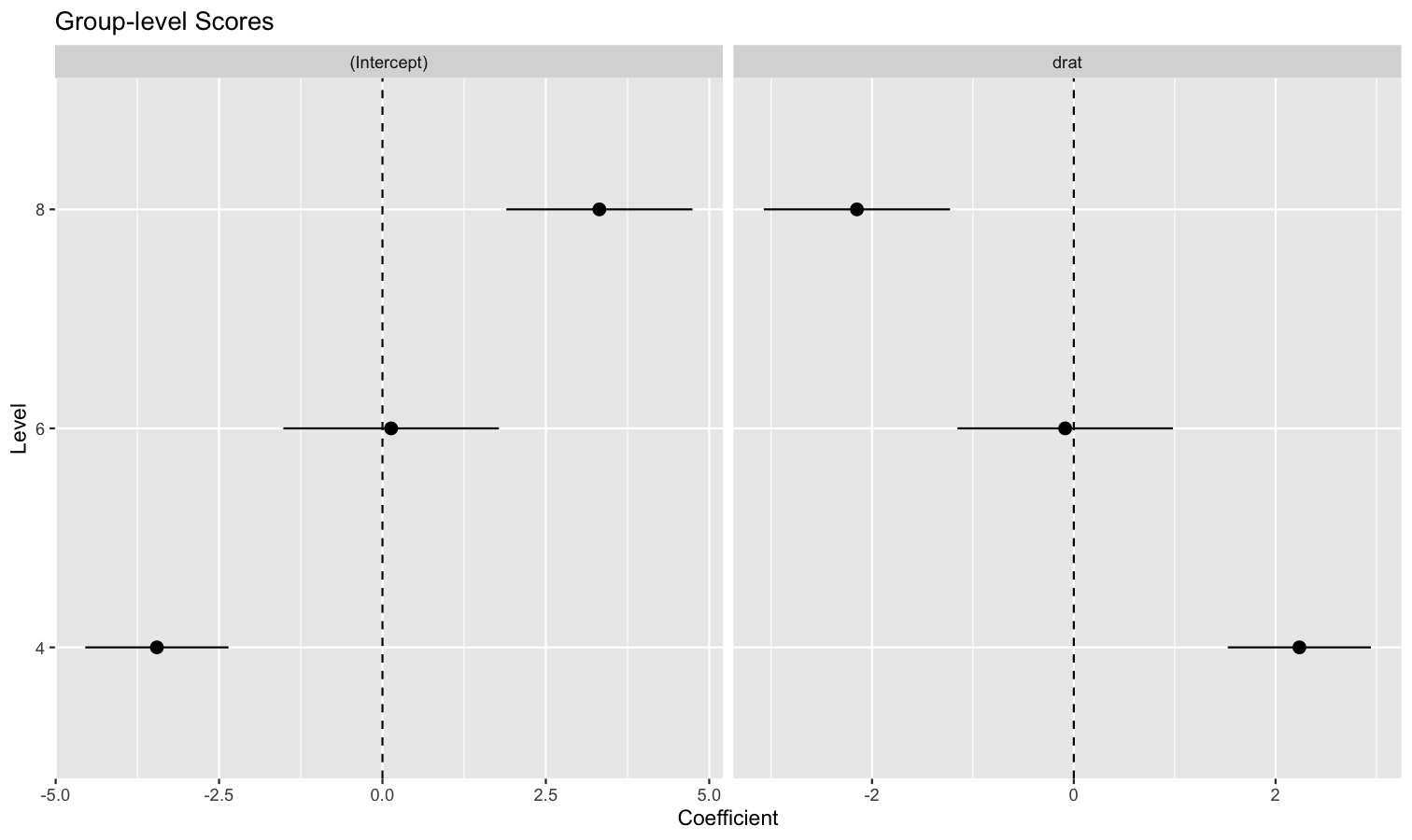
estimate_grouplevel on a mixed model.See this vignette for more information.
library(lme4)
model <- lmer(mpg ~ drat + (1 + drat | cyl), data = mtcars)
random <- estimate_grouplevel(model)
random
## Group | Level | Parameter | Coefficient | SE | 95% CI
## -----------------------------------------------------------------
## cyl | 4 | (Intercept) | -3.45 | 0.56 | [-4.55, -2.36]
## cyl | 4 | drat | 2.24 | 0.36 | [ 1.53, 2.95]
## cyl | 6 | (Intercept) | 0.13 | 0.84 | [-1.52, 1.78]
## cyl | 6 | drat | -0.09 | 0.54 | [-1.15, 0.98]
## cyl | 8 | (Intercept) | 3.32 | 0.73 | [ 1.89, 4.74]
## cyl | 8 | drat | -2.15 | 0.47 | [-3.07, -1.23]
plot(random) +
geom_hline(yintercept = 0, linetype = "dashed") +
theme_minimal()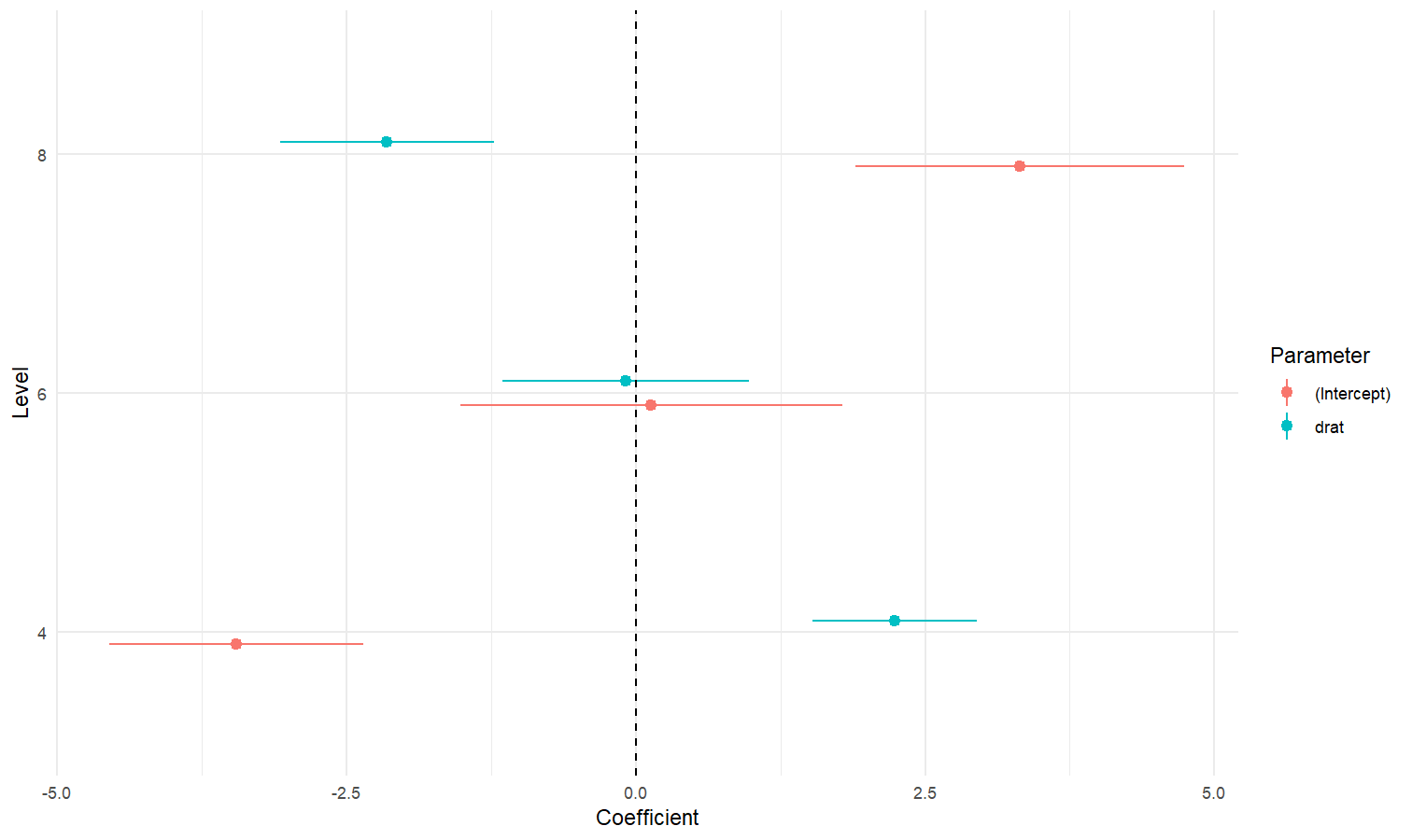
estimate_slopes.The two plots below represent the modeled (non-linear) effect estimated by the model, i.e., the relationship between the outcome and the predictor, as well as the “trend” (or slope) of that relationship at any given point. You can see that whenever the slope is negative, the effect is below 0, and vice versa, with some regions of the effect being significant (i.e., positive or negative with enough confidence) while the others denote regions where the relationship is rather flat.
Check-out this vignette for a detailed walkthrough on marginal effects.
library(patchwork)
# Fit a non-linear General Additive Model (GAM)
model <- mgcv::gam(Sepal.Width ~ s(Petal.Length), data = iris)
# 1. Compute derivatives
deriv <- estimate_slopes(model,
trend = "Petal.Length",
by = "Petal.Length",
length = 200
)
# 2. Visualize predictions and derivative
plot(estimate_relation(model, length = 200)) /
plot(deriv) +
geom_hline(yintercept = 0, linetype = "dashed")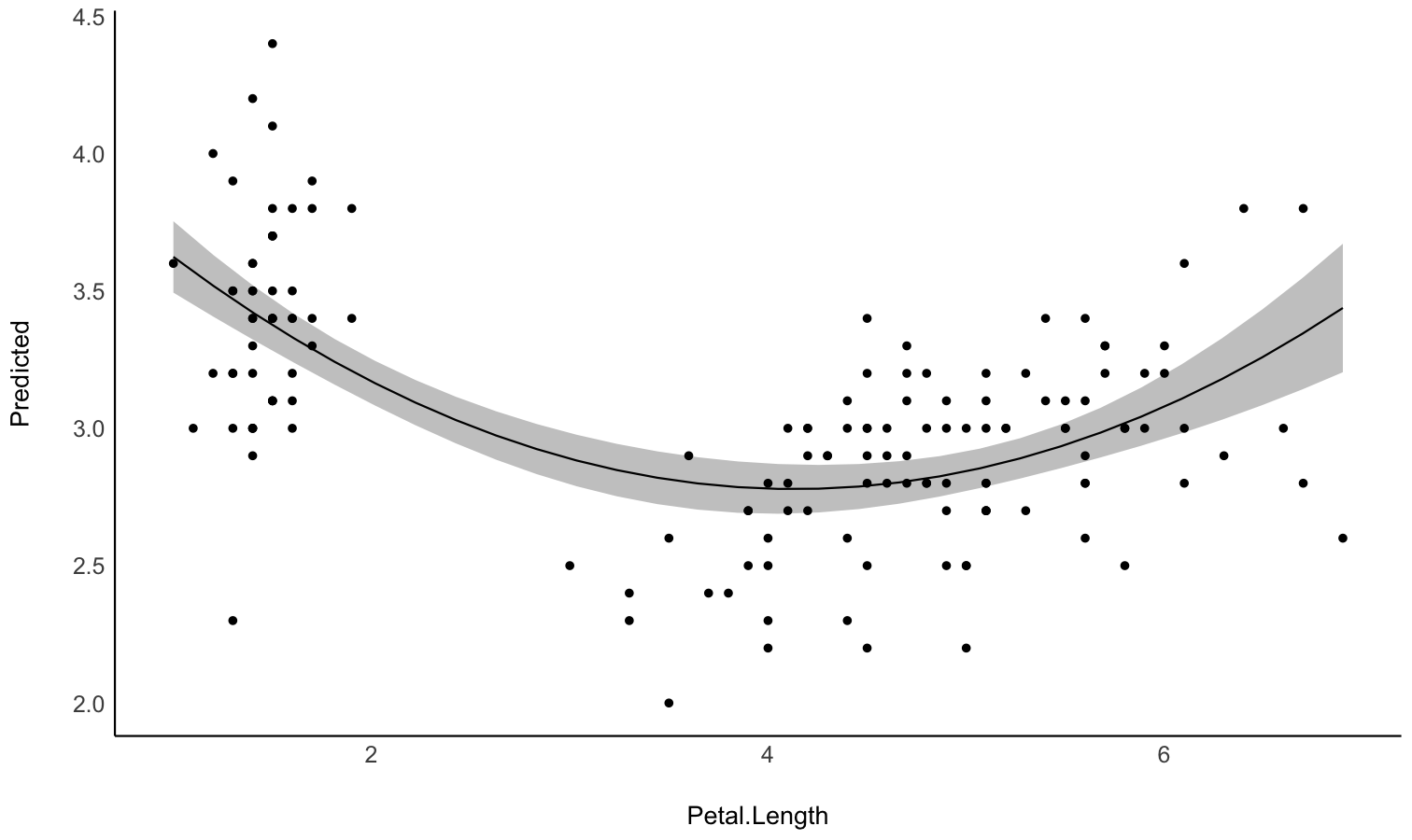
describe_nonlinear() on a predicted relationship that will
return the different parts of increase and decrease.model <- lm(Sepal.Width ~ poly(Petal.Length, 2), data = iris)
# 1. Visualize
vizdata <- estimate_relation(model, length = 30)
ggplot(vizdata, aes(x = Petal.Length, y = Predicted)) +
geom_ribbon(aes(ymin = CI_low, ymax = CI_high), alpha = 0.3) +
geom_line() +
# Add original data points
geom_point(data = iris, aes(x = Petal.Length, y = Sepal.Width)) +
# Aesthetics
theme_modern()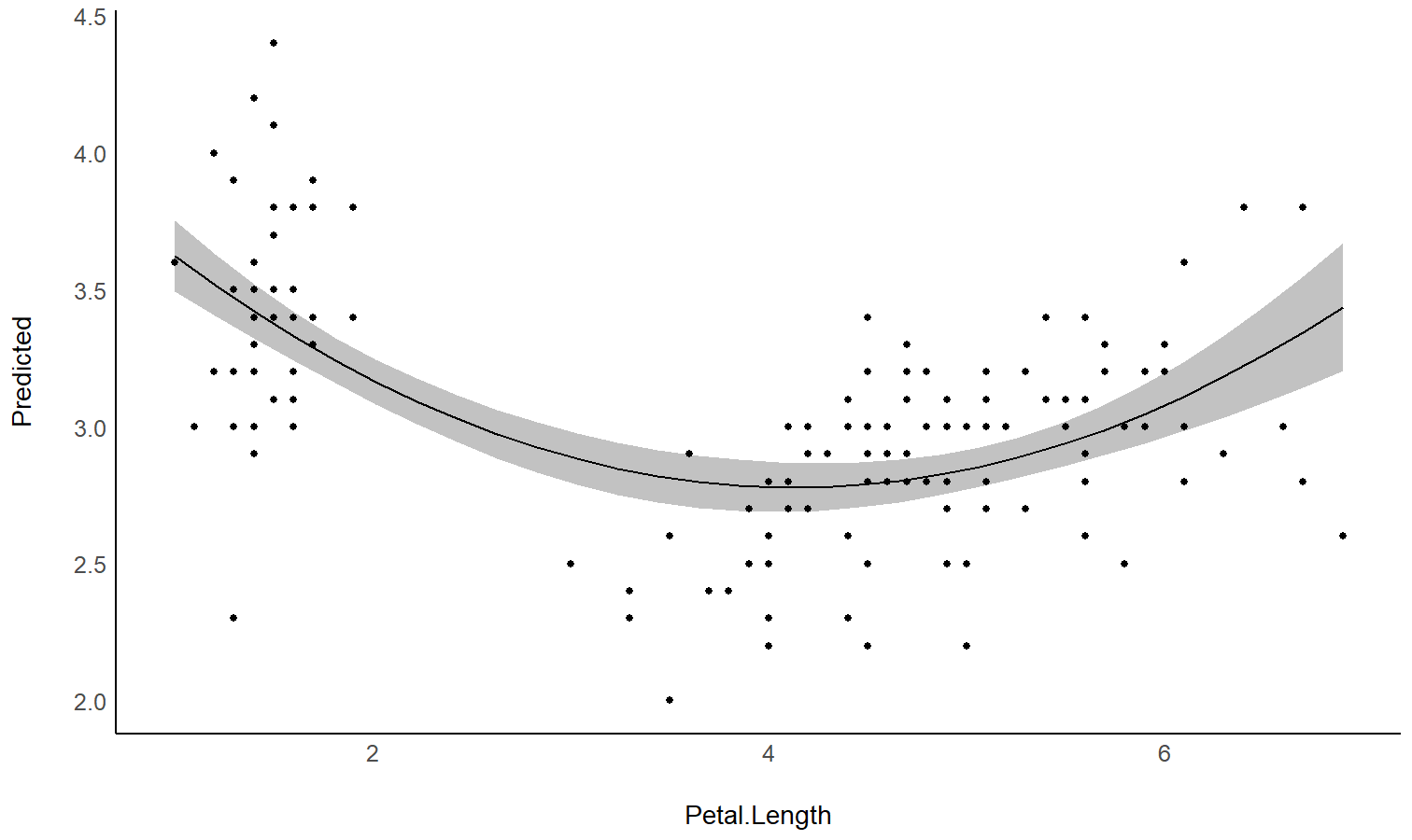
# 2. Describe smooth line
describe_nonlinear(vizdata, x = "Petal.Length")
## Start | End | Length | Change | Slope | R2
## ---------------------------------------------
## 1.00 | 4.05 | 0.50 | -0.84 | -0.28 | 0.05
## 4.05 | 6.90 | 0.47 | 0.66 | 0.23 | 0.05See this vignette for a walkthrough on how to do that.
Also referred to as Johnson-Neyman intervals, this plot shows how the effect (the “slope”) of one variable varies depending on another variable. It is useful in the case of complex interactions between continuous variables.
For instance, the plot below shows that the effect of hp
(the y-axis) is significantly negative only when wt is low
(< ~4).
model <- lm(mpg ~ hp * wt, data = mtcars)
slopes <- estimate_slopes(model, trend = "hp", by = "wt", length = 200)
plot(slopes)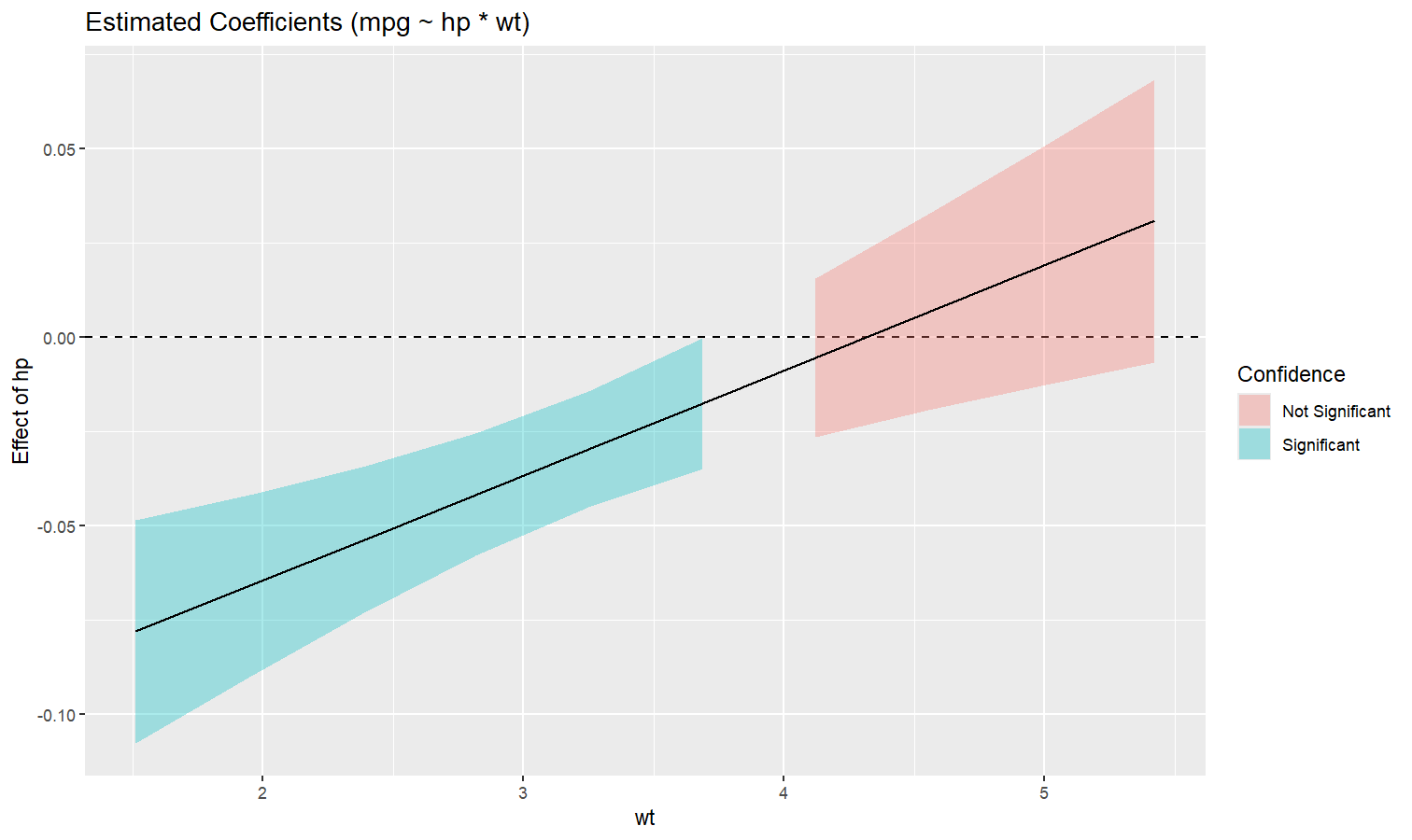
Aside from plotting the coefficient of each random effect (as done here),
we can also visualize the predictions of the model for each of these
levels, which can be useful to diagnostic or see how they contribute to
the fixed effects. We will do that by making predictions with
estimate_relation() and setting include_random
to TRUE.
Let’s model the reaction time with the number of days of sleep deprivation as fixed effect and the participants as random intercept.
library(lme4)
model <- lmer(Reaction ~ Days + (1 | Subject), data = sleepstudy)
preds <- estimate_relation(model, include_random = TRUE)
plot(preds, ribbon = list(alpha = 0)) # Make CI ribbon transparent for clarity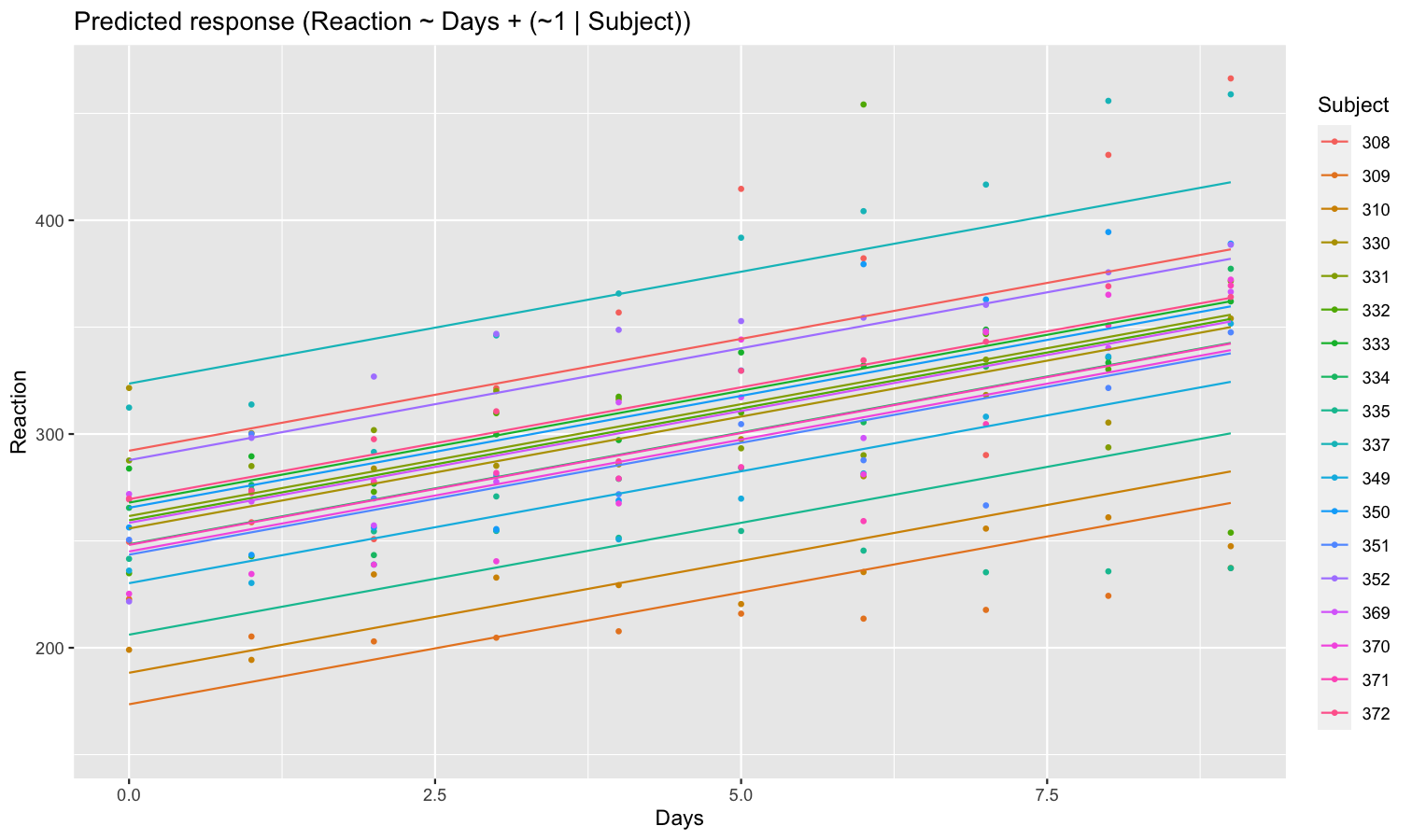
As we can see, each participant has a different “intercept” (starting point on the y-axis), but all their slopes are the same: this is because the only slope is the “general” one estimated across all participants by the fixed effect. Let’s address that and allow the slope to vary for each participant too.
model <- lmer(Reaction ~ Days + (1 + Days | Subject), data = sleepstudy)
preds <- estimate_relation(model, include_random = TRUE)
plot(preds, ribbon = list(alpha = 0.1))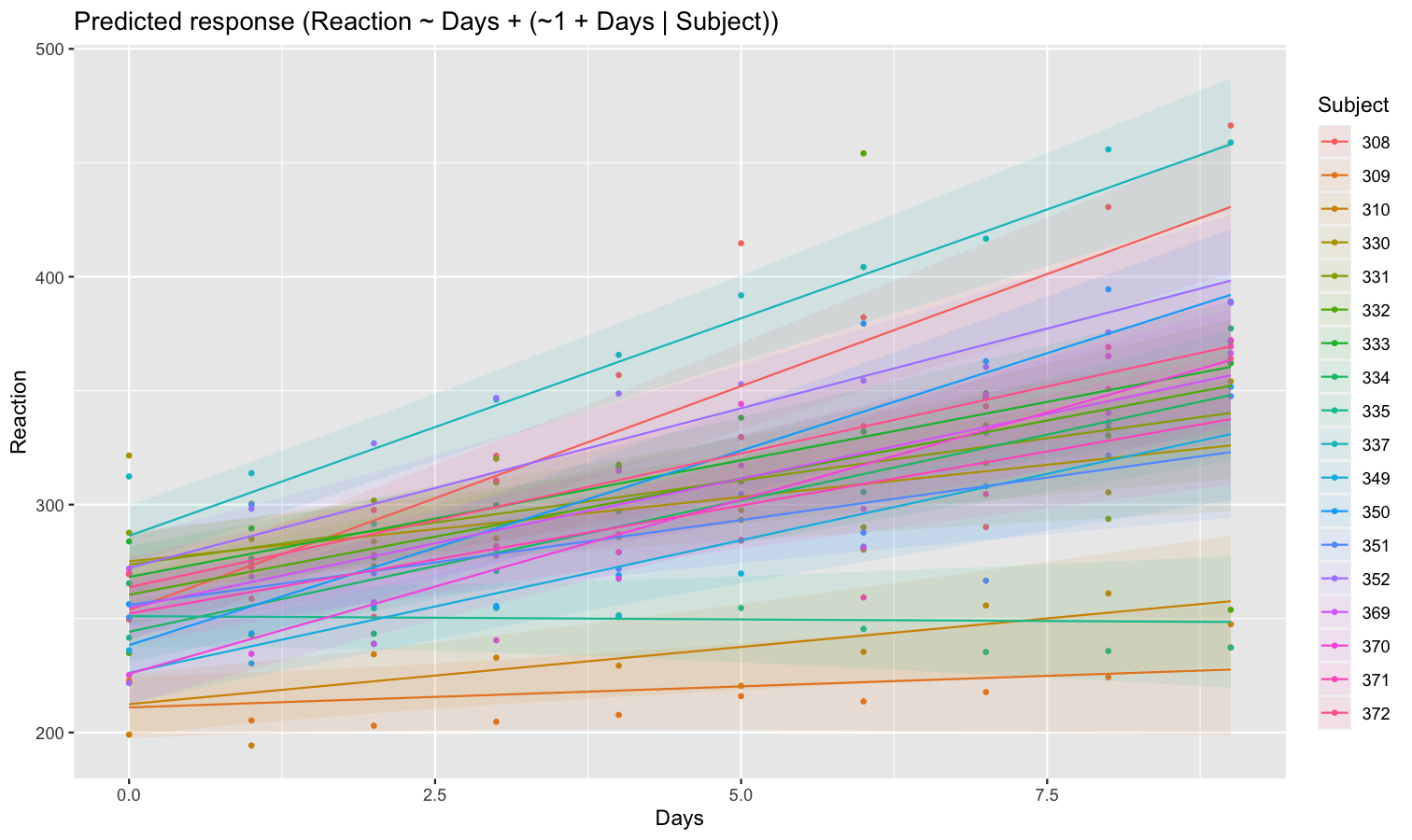
As we can see, the effect is now different for all participants. Let’s plot, on top of that, the “fixed” effect estimated across all these individual effects.
fixed_pred <- estimate_relation(model) # This time, include_random is FALSE (default)
plot(preds, ribbon = list(alpha = 0)) + # Previous plot
geom_ribbon(data = fixed_pred, aes(x = Days, ymin = CI_low, ymax = CI_high), alpha = 0.4) +
geom_line(data = fixed_pred, aes(x = Days, y = Predicted), linewidth = 2)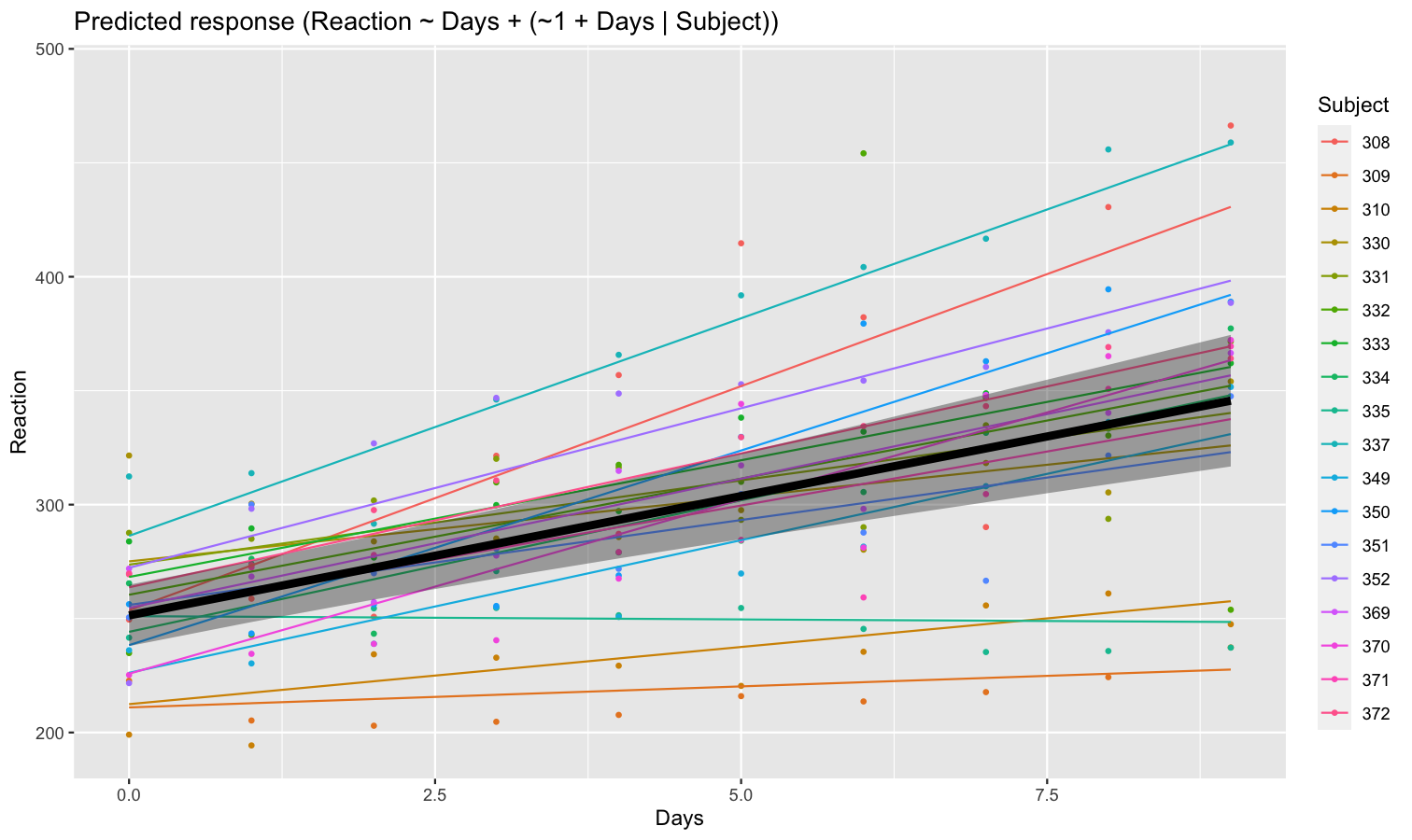
The algorithmic heavy lifting is done by {modelbased}’s
two back-end packages, {emmeans} and
{marginaleffects} (the default), which can be set as a
global option (e.g., with
options(modelbased_backend = "emmeans")).
Of the two, {emmeans} (Russell, 2024)
is the more senior package and was originally known as
{lsmeans} (for “Least-Squares Means”). This term has been
historically used to describe what are now more commonly referred to as
“Estimated Marginal Means” or EMMs: predictions made over a regular
grid—a grid typically constructed from all possible combinations of the
categorical predictors in the model and the mean of numerical
predictors. The package was renamed in 2016 to {emmeans} to
clarify its extension beyond least-squares estimation and its support of
a wider range of models (e.g., Bayesian models).
Within {emmeans}, estimates are generated as a linear
function of the model’s coefficients, with standard errors produced in a
similar manner by taking a linear combination of the coefficients’
variance-covariance matrix. For example if \(b\) is a vector of 4 coefficients, and
\(V\) is a 4-by-4 matrix of the
coefficients’ variance-covariance, we can get an estimate and SE for a
linear combination (or set of linear combinations) \(L\) like so:
\[ \hat{b} = L \cdot b \]
\[ SE_{\hat{b}} = \sqrt{\text{diag}(L \cdot V \cdot L^T)} \]
These grid predictions are sometimes averaged over (averaging being a
linear operation itself) to produce “marginal” predictions (in the sense
of marginalized-over): means. These predictions can then be contrasted
using various built-in or custom contrasts weights to obtain meaningful
estimates of various effects. Using linear combinations with regular
grids often means that results from {emmeans} directly
correspond to a models coefficients (which is a benefit for those who
are used to understanding models by examining coefficient tables).
{marginaleffects} (Arel-Bundock et al.,
2024) was more recently introduced and also relies on the Delta
method, but uses numeric differentiation (and can easily switch to
bootstrap or simulation-based approaches). By default, it estimates
various effects by generating two counter-factual predictions of
unit-level observations, then taking the difference between them - which
can easily be done on the response scale, rather than the link scale.
Because these effects are calculated for every observation, they can
then be averaged (e.g., as an Average Treatment Effect). This approach
is more iterative compared to the linear matrix multiplication used by
{emmeans}, but is similarly efficient.
While both packages employ the Delta method to obtain standard errors
on transformed scales, they differ in how they construct and average
predictions. {emmeans} often produces effects at the
mean of non-focal predictors (via linear contrasts), whereas
{marginaleffects} tends to compute mean effects by
averaging over observations. Depending on the model and the type of
quantity you want to estimate, results from these two approaches can be
very similar—or differ in interesting ways.
Note that {emmeans} can also perform numeric
differentiation or use non-regular grids, just as
{marginaleffects} can construct linear predictions at the
mean. Because each package has evolved with slightly different
philosophies regarding how to form and interpret predictions, users can
select whichever approach best suits their research questions. In
{modelbased}, you can switch easily between either back end
by setting the global option, for example
options(modelbased_backend = "marginaleffects"), to access
these features.
Finally, {modelbased} leverages the
get_datagrid() function from the {insight}
package (Lüdecke et al.,
2019) to intuitively generate an appropriate grid of data points for
which predictions or effects or slopes will be estimated. Since these
packages support a wider range of models - including generalized linear
models, mixed models, and Bayesian models - {modelbased}
also inherits the support for such models.
If this package helped you, please consider citing as follows:
Makowski, D., Ben-Shachar, M. S., Wiernik, B. M., Patil, I., Thériault, R., & Lüdecke, D. (2025). modelbased: An R package to make the most out of your statistical models through marginal means, marginal effects, and model predictions. Journal of Open Source Software, 10(109), 7969. doi: 10.21105/joss.07969
Please note that the modelbased project is released with a Contributor Code of Conduct. By contributing to this project, you agree to abide by its terms.