The objective of plsmmLasso is to facilitate the estimation of a Regularized Partial Linear Semiparametric Mixed-Effects Model (PLSMM) through a dictionary approach for modeling the nonparametric component. The model employs a set of bases functions and automatically selects them using a lasso penalty. Additionally, it conducts variable selection on the fixed-effects using another lasso penalty. The implementation also supports the inclusion of a random intercept.
You can install the development version of plsmmLasso from GitHub with:
# install.packages("devtools")
devtools::install_github("Sami-Leon/plsmmLasso")Here’s a basic example using a simulated dataset to demonstrate how to utilize the main functions of the plsmmLasso package. This example assumes an effect of a grouping variable and different nonlinear functions for each group.
library(plsmmLasso)
# Simulate a dataset
set.seed(123)
data_sim <- simulate_group_inter(
N = 50, n_mvnorm = 3, grouped = TRUE,
timepoints = 3:5, nonpara_inter = TRUE,
sample_from = seq(0, 52, 13),
cos = FALSE, A_vec = c(1, 1.5)
)
sim <- data_sim$sim
# Fit the data
x <- as.matrix(sim[, -1:-3])
y <- sim$y
series <- sim$series
t <- sim$t
bases <- create_bases(t)
lambda <- 0.0046
gamma <- 0.00001
plsmm_output <- plsmm_lasso(x, y, series, t,
name_group_var = "group", bases$bases,
gamma = gamma, lambda = lambda, timexgroup = TRUE,
criterion = "BIC"
)One of the most important output of the plsmm_lasso()
function is the estimates of the fixed-effects.
plsmm_output$lasso_output$theta
#> Intercept group x1 x2 x3 x4 x5
#> 0.19729689 3.15155151 1.91905369 0.74891414 0.02274130 0.01291499 0.01049015Here, we observe that some covariates have small values, but most are non-zero. If we desire more regularization for the fixed-effects, we can use a larger value for lambda.
lambda <- 0.1
plsmm_output <- plsmm_lasso(x, y, series, t,
name_group_var = "group", bases$bases,
gamma = gamma, lambda = lambda, timexgroup = TRUE,
criterion = "BIC"
)
plsmm_output$lasso_output$theta
#> Intercept group x1 x2 x3 x4 x5
#> 3.5544003 0.4262652 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000With a larger lasso penalty, more coefficients are set to zero.
The coefficients associated with the nonlinear functions are denoted by alpha.
head(plsmm_output$lasso_output$alpha)
#> [1] -5.576108e-02 -4.720350e-01 -8.130512e-03 2.368476e-10 -7.129181e-06
#> [6] 0.000000e+00Similar behavior would be observed for the alpha values if we were to increase the value of gamma.
To find optimal values for gamma and lambda, we tune these
hyperparameters using BIC-type criteria with the
tune_plsmm() function and a grid search.
lambdas <- gammas <- round(exp(seq(log(1), log(1 * 0.00001),
length.out = 5
)), digits = 5)
tuned_plsmm <- tune_plsmm(x, y, series, t,
name_group_var = "group", bases$bases,
gamma_vec = gammas, lambda_vec = lambdas, timexgroup = TRUE,
criterion = "BIC"
)The tune_plsmm() function tries every possible
combination of the values from lambdas and gammas and returns the model
with the best BIC (other options are BICC and EBIC). This example is for
illustration purposes only; in practice, a more exhaustive grid should
be used.
The plot_fit() function allows for the visualization of
the estimated mean trajectories as well as the estimate of the nonlinear
functions. By default, only the observed time points are being used. To
use continuous time points, the argument predicted can be
set to TRUE.
plot_fit(x, y, series, t, name_group_var = "group", tuned_plsmm)
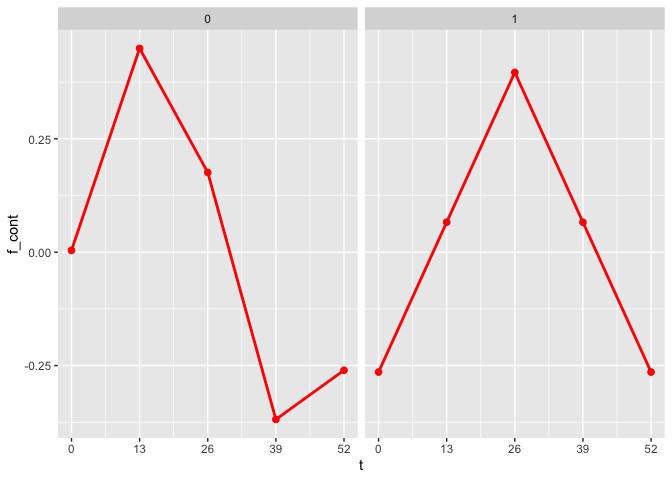
plot_fit(x, y, series, t, name_group_var = "group", tuned_plsmm, predicted = TRUE)

To compute p-values on the fixed-effects, the
debias_plsmm() function can be used.
debias_plsmm(x, y, series, tuned_plsmm)
#> Estimate Debiased Std. Error Lower 95% Upper 95% p-value
#> group 3.20441442 3.31447827 0.33608394 2.65575376 3.9732028 6.079223e-23
#> x1 1.95569696 2.03694234 0.21339004 1.61869786 2.4551868 1.352832e-21
#> x2 0.72925412 0.68895582 0.26577859 0.16802979 1.2098818 9.535955e-03
#> x3 0.02755599 0.03780433 0.04645279 -0.05324313 0.1288518 4.157466e-01
#> x4 0.01691564 0.02535323 0.04110770 -0.05521786 0.1059243 5.373988e-01
#> x5 0.01569818 0.02732562 0.04056090 -0.05217374 0.1068250 5.005061e-01The function reports the original coefficients, debiased coefficients, standard errors, confidence intervals and p-values. These p-values are already adjusted for the selection process of the lasso, and provide valid inference.
Finally, we can perform tests on the nonlinear functions. The first element of the list is an overall test of equality. If the p-value is \(< 0.05\), we reject the null hypothesis of equality and conclude that overall the two nonlinear functions are different. To obtain a comparison at each time point, confidence bands are computed, and a figure displaying these confidence bands is generated. For the time points associated with confidence bands that include \(0\), we cannot reject the null hypothesis that the nonlinear functions are the same for this time point. The data frame that is used to generate this figure can be found in the second element of the output list.
test_f_results <- test_f(x, y, series, t,
name_group_var = "group", tuned_plsmm,
n_boot = 10, verbose = TRUE
)
#> | | | 0% | |======= | 10% | |============== | 20% | |===================== | 30% | |============================ | 40% | |=================================== | 50% | |========================================== | 60% | |================================================= | 70% | |======================================================== | 80% | |=============================================================== | 90% | |======================================================================| 100%
#>
#> Completed fitting Bootstrap samples. Now formatting results, and generating figure.
test_f_results[[1]]
#> T p-value
#> 1 0.4785269 0
head(test_f_results[[2]])
#> t f diff. Lower 95% Upper 95%
#> 1 0.0 0.2365327 0.00586791 0.4414301
#> 2 0.1 0.2400843 0.01051297 0.4443028
#> 3 0.2 0.2436013 0.01512247 0.4471456
#> 4 0.3 0.2470832 0.01969562 0.4499582
#> 5 0.4 0.2505294 0.02423163 0.4527404
#> 6 0.5 0.2539394 0.02872971 0.4554919Similarly to the plot_fit() function, the argument
predicted can be changed to TRUE to display
the joint confidence bands as a continuous function of time rather than
at the observed time points only.
test_f_results <- test_f(x, y, series, t,
name_group_var = "group", tuned_plsmm,
n_boot = 10, predicted = TRUE
)
#> | | | 0% | |======= | 10% | |============== | 20% | |===================== | 30% | |============================ | 40% | |=================================== | 50% | |========================================== | 60% | |================================================= | 70% | |======================================================== | 80% | |=============================================================== | 90% | |======================================================================| 100%
#>
#> Completed fitting Bootstrap samples. Now formatting results, and generating figure.
The plsmmLasso package offers flexibility; if the nonlinear functions
do not differ between groups, the timexgroup argument can
be set to FALSE. Below, we simulate a dataset where the
nonlinear functions are the same and fit the data accordingly.
# Simulate a dataset with equal nonlinear functions per group
set.seed(123)
data_sim <- simulate_group_inter(
N = 50, n_mvnorm = 3, grouped = TRUE,
timepoints = 3:5, nonpara_inter = FALSE,
sample_from = seq(0, 52, 13),
cos = FALSE, A_vec = c(1, 1.5)
)
sim <- data_sim$sim
# Fit the data
x <- as.matrix(sim[, -1:-3])
y <- sim$y
series <- sim$series
t <- sim$t
bases <- create_bases(t)
tuned_plsmm <- tune_plsmm(x, y, series, t,
name_group_var = "group", bases$bases,
gamma_vec = gammas, lambda_vec = lambdas, timexgroup = FALSE,
criterion = "BIC"
)
plot_fit(x, y, series, t, name_group_var = "group", tuned_plsmm)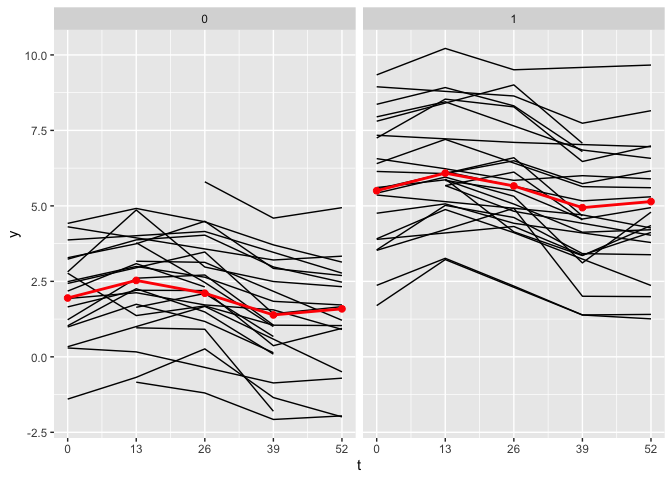

As observed, the estimates of the nonlinear functions are identical.
It is also possible not to use any grouping variable for the
name_group_var argument. Here, we simulate a dataset
without the effect of a grouping variable, resulting in no difference in
the height of the overall mean trajectories and using the same nonlinear
functions.
# Simulate a dataset with no group effect
set.seed(123)
data_sim <- simulate_group_inter(
N = 50, n_mvnorm = 3, grouped = FALSE,
timepoints = 3:5, nonpara_inter = FALSE,
sample_from = seq(0, 52, 13),
cos = FALSE, A_vec = c(1, 1.5)
)
sim <- data_sim$sim
# Fit the data
x <- as.matrix(sim[, -1:-3])
y <- sim$y
series <- sim$series
t <- sim$t
bases <- create_bases(t)
tuned_plsmm <- tune_plsmm(x, y, series, t,
name_group_var = NULL, bases$bases,
gamma_vec = gammas, lambda_vec = lambdas, timexgroup = FALSE,
criterion = "BIC"
)
plot_fit(x, y, series, t, name_group_var = NULL, tuned_plsmm)

Only one figure is displayed now since there is no grouping variable.